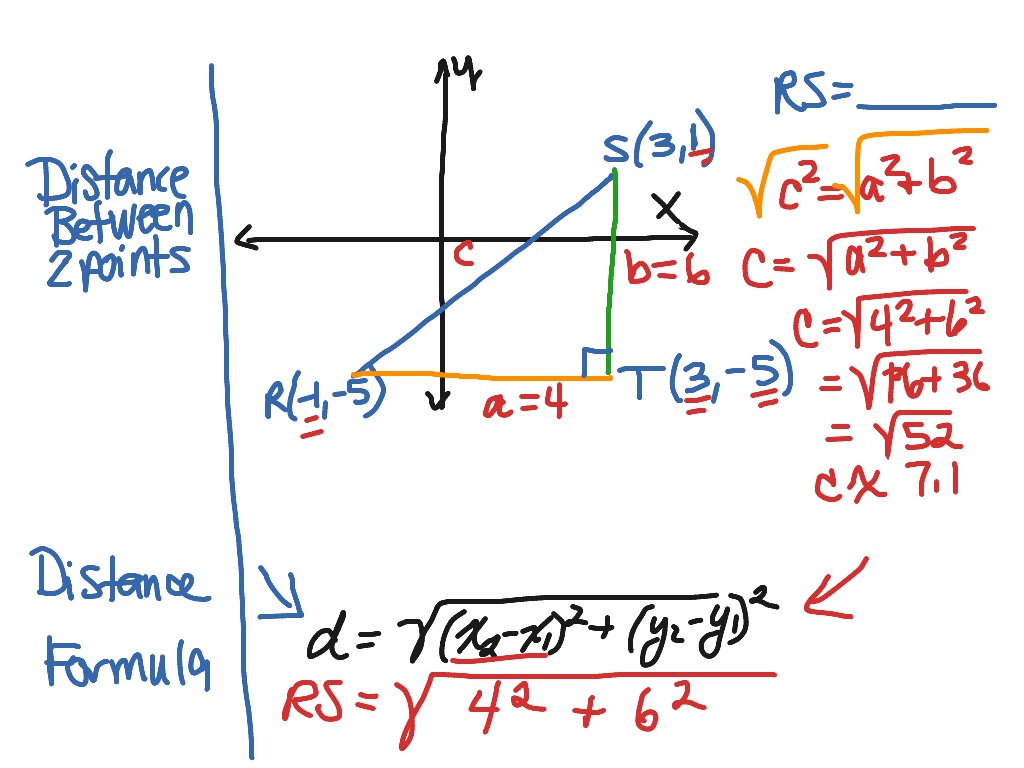
lobiti.blogg.se - Distance formula geometry

#Distance formula geometry plus#

This is quite easy, because the two points lie on the horizontal line #y=3#, so the distance between them can be interpreted as the length of the line segment #AB#, which is #5# and can be computed by subtracting the #x#-coordinates of the two points and considering the absolute value of the result (to avoid negative distances). a plane with a coordinate system such that).įirst of all, let's compute the distance between #A=(2,3)# and #B=(7,3)#. It's used to compute the distance between two points in an orthogonal coordinate system (i.e. The distance formula makes sense in a coordinate context. In other words, they are the same thing in two seemingly different contexts. In short, the distance formula is a formalization of the Pythagorean Theorem using #x# and #y# coordinates. (depending on if #x_1 > x_2# or #x_1 < x_2#, and similarly for #y#.) Or, we could put it another way through substitutions based on the distance definitions above. What do you see in these formulas? Have you ever tried drawing a triangle on a Cartesian coordinate system? If so, you should see that these are two formulas relating the diagonal distance on a right triangle that is composed of two component distances #x# and #y#. The greater the #x# contribution, the flatter the slope. The greater the #y# contribution, the steeper the slope.

Any diagonal line segment has an #x# component and a #y# component, due to the fact that a slope is #Deltay"/"Deltax#.

The distance from one point to another is the definition of a line segment.

There is the relationship where #sqrt((x-c)^2) = color(green)(|x-c|) = x-c " AND " -x+c#.

The definition of a distance from #x# to #pmc# is #color(green)(|x-c|)#.

We commonly write the Pythagorean Theorem as:Ĭonsider the following major points (in Euclidean geometry on a Cartesian coordinate axis): The distance formula is commonly seen as: Together with magic, they also enabled him to predict future events.If we consider what the distance formula really tells you, we can see the similarities. He believed that Mathematics and numbers governed life and afterlife. Later, he established the religion Pythagoreanism. Pythagoras’ fondness for numbers was mixed with his delight for magic. Scores of other philosophers and scientists were likewise influenced by the distance formula inventor. In fact, Plato was so influenced by Pythagoras’ ideas. But his contribution to Geometry and Trigonometry was exemplary. Pythagoras was said to have learned basic Geometry from the Egyptians-the famed Pyramid builders, Arithmetic from the Phoenicians, and Astronomy from the Babylonians.

Architects, engineers, pilots, and seamen use it in their works. The Pythagorean Theorem is a vital formula in Geometry and Trigonometry. The man who invented the distance formula figured any unknown value of this equation can be solved by merely manipulating or transposing the formula. According to the distance formula inventor, C is the value for the base, A is the value for the height, and B is the value for the hypotenuse side.

#Distance formula geometry plus#

The formula for this is C squared is equal to A squared plus B squared. Thus, to solve the distance from one point to a standing structure, and the dimensions for the structure height and the hypotenuse are given, the distance can be calculated.

If 2 sides have known dimensions the third unknown can be solved. This triangle has three sides-the base, the height, and the hypotenuse, which is the diagonal side. Vertical, horizontal, or diagonal distance can be solved using Pythagoras distance formula, or what is called “Pythagorean theorem.” The man who invented the distance formula based this on the dimensions of a right triangle or a 90 degree triangle. He was also fond of experimenting with numbers and later on ended up being the distance formula inventor. According to records, he was much amazed by what knowledge was available in Egypt. He traveled not just to Egypt and Babylon, but also to Arabia, Phoenicia, Judea, and India. He was from Samos and born around 570 B.C. Many acknowledge that Pythagoras was the person who invented the distance formula. Aside from being educated in Greece, the distance formula inventor traveled other parts of the world to learn from other civilizations. He was a scientist and a philosopher always seeking the meaning in life. The man who invented the distance formula must have been amazed by distances.